Зависимые источники сигналов
Зависимые источники напряжения и тока могут быть как линейными, так и нелинейными. Существует четыре их разновидности:
v =
e(v)
- источник напряжения, управляемый напряжением (ИНУН);
i
=
f(i)
- источник тока, управляемый током (ИТУТ);
i
=
g(v)
- источник тока, управляемый напряжением (ИТУН);
v =
h(i)
- источник напряжения, управляемый током (ИНУТ).
Линейные управляемые источники
описываются зависимостями v =
ev, i = fi, i = gv,
v =
hi,
где
е, f, g
и
h
- коэффициенты передачи.
В описании
нелинейных зависимых источников у
=
у(х
1
, х
2
,
...,
х
п
)
используется полиномиальная функция POLY вида
У = P
0
+ P
1
x
1
+ P
2
x
2
+...+
P
n
x
n
...
Здесь
х
1
, х
г
, ..., х
п
-
п
управляющих переменных. Они могут быть токами или разностью потенциалов; одновременное управление током и разностью потенциалов не допускается. Все коэффициенты полинома Я вводить не обязательно, но вводить их необходимо подряд без пропусков. При одномерном управлении
(п =
1) допускается следующая форма полинома
у(х):
При п = 2 полином приобретает вид
y = Р
0
+
P
1
x
1
+
Р
2
х
2
+ P
3
x
2
1
+ Р
4
х
1
х
2
+ Р
5
х
2
Рассмотрим подробно все четыре типа зависимых источников.
Источник напряжения, управляемый напряжением
(ИНУН), задается предложениями:
1)
линейный источник:
Еххх <+узел> <-узел> <+управляющий узел> <-управляющий узел> + <коэффициент передачи>
2)
нелинейный источник:
Еххх <+узел> <-узел>
POLY(<n>)<< +
управляющий узел> + <-управляющий узел>>* + <коэффициент полинома>*
Например, линейный источник
ELIN=2,5V
10.11
описывается предложением
ELIN121011 2.5
Нелинейный источник
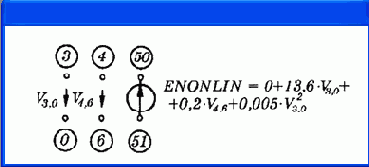
ENONLIN
= 0 + 13,6V
3,0
+ 0,2V
4,6
+ 0,0051V
3,0
(рис. 4.16, a)- предложением
ENONLIN 50 51 POLY(2) (3,0) (4,6) 0.0 13.6 0.2 0.005
Источник тока, управляемый током
(ИТУТ), задается следующим образом:
1)
линейный источник:
Fxxx <+узел> <-узел> <имя управляющего источника напряжения> + <коэффициент передачи>
2)
нелинейный источник:
Fxxx <+узел> <-узел>
POLY(<n>)
+
<имя управляющего источника напряжения>*
+ <коэффициент полинома>*
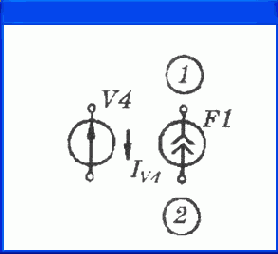
Управляющим током служит ток независимого источника напряжения. Например, линейный источник тока
F1=7,5I
V4
(рис. 4.16,
б)
описывается предложением .
F1 2 1 V4 7.5
Нелинейный источник тока -
FNONLIN
= 0,01 + 13,6I
VС1
+ 0,2I
VС2
+ 0,0054, + 0,001I
VC1
I
VС2
предложением
FNONLIN1011 POLY(2)VC1 VC2 0.01 13.60.20.0050.001
а)
б)
Рис. 4.16. Нелинейный (а) источник напряжения, управляемые напряжением, и линейный источник тока, управляемый током (б)
Источник тока, управляемый напряжением
(ИТУН), задается предложениями:
1)
линейный источник:
Gxxx <+узел> <-узел> <+управляющий узел> <-управляющий узел> + <коэффициент передачи>
2)
нелинейный источник:
Gxxx <+узел> <-узел>
POLY(<n>)
«+управляющий узел> + <-управляющий узел>>* <коэффициент полинома>*
Источник напряжения, управляемый током
(ИНУТ), задается следующим образом:
1)
линейный источник:
Нххх <+узел> <-узел> <имя управляющего источника напряжения> + <коэффициент передачи>
2)
нелинейный источник:
Нххх <+узел> <-узел>
POLY(<m>)
+
<имя управляющего источника напряжения>*
+ <коэффициент полинома>*
Замечание.
В связи с тем, что в описаниях линейных управляемых источников не допускается использование параметров и функций, в этих целях можно воспользоваться зависимыми источниками с нелинейными передаточными функциями (см. п. 4.2.5).
Одно из применений нелинейных зависимых источников - генерация
ампли-тудно-модулированных сигналов.
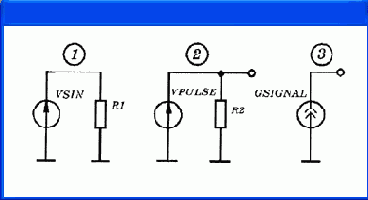
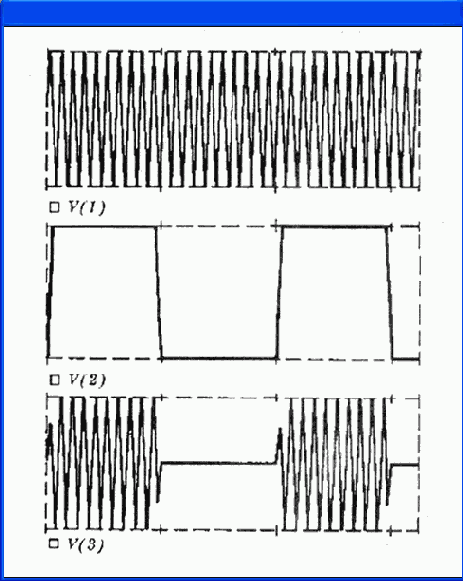
В качестве примера на рис. 4.17, а показана схема создания источника радиоимпульсов, а на рис. 4.17,
б
- эпюры напряжений, полученные в результате выполнения следующего задания на моделирование:
RADIOSIGNAL
VSIN 1 OSIN(0 1 100)
VPULSE 2 О PULSE(0 1 0 0.25 0.25 0.5 1)
GSIGNAL 0 3 POLY(2)(1,0)(2,0) 00001
R1101MEG
R2201MEG
R3301MEG
.IRAN 0.01 1.6
.PROBE V(1)V(2)V(3)
.END
Здесь VSIN - источник гармонического сигнала с частотой 100 Гц; VPULSE - источник импульсного напряжения с периодом повторения 1 с. Перемножение этих сигналов с помощью нелинейного источника тока GSIGNAL создает последовательность радиоимпульсов.
Наличие зависимых источников позволяет моделировать не только электрические принципиальные схемы, но и
функциональные схемы
динамических систем с обратными связями, а также решать
системы дифференциальных уравнений.
а)
б)
Рис. 4.17. Формирование последовательности радиоимпульсов: а - формирователь сигнала; б - эпюры напряжений
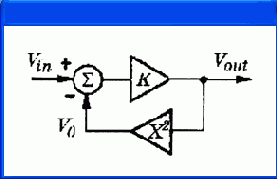
Рассмотрим в качестве примера
усилитель постоянного тока с квадратором в цепи обратной связи,
функциональная схема которого показана на рис. 4.18,
а.
При бесконечно большом коэффициенте передачи усилителя
К
->бесконечности выходное напряжение
V
out
= (V
in
)
1/2
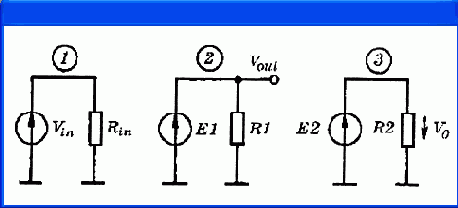
Составим схему замещения этого усилителя, используя компоненты, разрешенные в программе PSpice (рис. 4.18,
б).
С помощью нелинейного источника Е1 осуществляется вычитание напряжений
V
in
, V
0
и усиление разностного сигнала в
К
раз. Выходное напряжение
V
ou
,
возводится в квадрат с помощью нелинейного источника
Е2.
Каждый источник напряжения замкнут на большое сопротивление, чтобы в схеме замещения не было разомкнутых контуров. На входном языке программы PSpice схема замещения описывается следующим образом:
Rin 1 О 1MEG
Е1 2 О POLY(2) (1,0) (3,0) О 1Е6 -1Е6; усилитель-сумматор
R1201MEG
Е2 3 О POLY(2) (2,0) (2,0) 00001; квадратор
R2301MEG
а)
б)
Рис. 4.18. Моделирование функциональных схем: а - устройство вычисления квадратного корня; б - эквивалентная принципиальная схема для PSpice
Замечание.
Отметим, что наличие в схемном редакторе PSpice Schematics библиотеки символов функциональных блоков amb.slb позволяет не составлять электрические схемы замещения функциональных схем типа рис. 4.18, б, а сразу составлять функциональные схемы из имеющихся стандартных функциональных блоков (см. Приложение 1 [7]).
Продемонстрируем методику решения
дифференциальных уравнений
на примере системы уравнений
dx
1
/dt=-0,3
x
l
+x
2
+x
1
2
-3х
1
х
2
-x
1
dx
2
/dt= 0,24 - 0,6x
2
+ 4x
1
x
2
- 6x
1
2
x
2
at
с
начальными условиями х
1
(0) = 0, х
2
(0) = 0,4. Используя уравнение конденсатора i =
Cdu/dt,
смоделируем систему дифференциальных уравнений с помощью зависимых источников тока
GX1, GX2,
подключенных к конденсаторам
C1, C2,
как показано на рис. 4.19. На входном языке программы PSpice задание на моделирование составляется следующим образом:
DIFFERENTIAL EQUATIONS
GX1 0 1 POLY(3) (1,0) (2,0) (0,0) 0 -0.3 101-300001
GX2 0 2 POLY(3) (1,0) (2,0) (0,0) 0.6 0 -0.6 00400000-6
С1 1 01
С2201
.ICV(1)=OV(2)=0.4
.IRAN 0.1s 40s SKIPBP
Переменные
x
1
= V(l), x
2
= V(2).
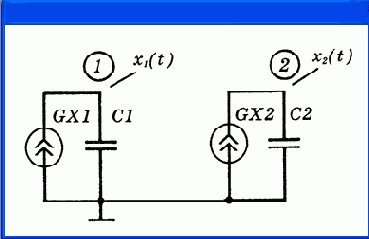
Рис. 4.19. Моделирование системы двух дифференциальных уравнений
<
