Устойчивость

Для каждого указанного пользователем загружения (или комбинации загружений) SCAD позволяет определить:

• коэффициент запаса устойчивости;
• первую форму потери устойчивости (без анализа кратности);

свободные длины стержневых элементов.

13.1 Постановка задачи

Задача устойчивости решается в классической постановке для упругой системы и в предположении, что все приложенные к системе внешние нагрузки (следовательно, и внутренние силы) растут пропорционально одному и тому же параметру l. То значение параметра l, при котором матрица жесткости системы А(l) впервые  перестает быть положи­тельно определенной, является критическим, а соответ­ствующее значение l — коэффициентом запаса устойчивости (КЗУ). Матрица жесткости А(l) = Ao

- B(l) состоит из “обычной” матрицы жесткости Ao и матрицы “толкающих” реакций B(l), которые определяются сжимающими силами в стержнях, напряжениями сжатия в конечных элементах оболо­чечного типа и т.п. Напоминаем, что положительная опреде­лен­ность матрицы жесткости означает, что при любых значениях узловых перемещений и поворотов u потенциальная энергия системы положительна (это значит, что для деформирования системы необходимо затратить энергию и, следовательно, она оказывает сопротивление деформированию, она является отпорной).

                Если система теряет устойчивость, она теряет отпорность и ее матрица жесткости становится вырожденной (с нулевым детерминантом), а в закритическом состоянии система получает отрицательную отпорность (при ее принуди­тельном деформировании выделяется ранее накопленная потенциальная энергия “толкающих” реакций) и ее матрица жесткости становится знаконеопределенной.

                Таким образом, задача оценки устойчивости равно­весия сводится к проверке положительной определен­ности матрицы жесткости при пробном значении коэффициента l.

                Необходимо отметить, что с помощью проверок матрицы жесткости можно отыскать только те критические состояния, при которых потеря устойчивости происходит по форме, когда узловые перемещения и повороты не все вместе равны нулю (это так называемая явная форма потери устойчивости). Нужно еще проверить, что при пробном значении l не может произойти так называемая скрытая форма потери устойчивости, которая реализуется в пределах одного конечного элемента и не вызывает узловых перемещений и поворотов. Поскольку для всех типов конечных элементов соответствующие критические величины lкр известны (они вычисляются по простым формулам), то это значит, что следует, кроме всего прочего, проверить неравенство l > lкр для всех конечных элементов.


13.2 Поиск коэффициента запаса устойчивости

Поиск коэффициента запаса устойчивости (КЗУ) ведется в интервале [0,L], где L ? число, заданное пользователем, ( оценка того значения КЗУ, которое считается уже безразличным для оценки качества системы) и с точностью e, которая также задается пользователем.

                При этом решается задача определения минимального l, при котором происходит вырождение матрицы А(l).

                Матрица А(l) составляется из матриц устойчивости отдельных конечных элементов. Если в системе нет ни одного элемента, способного терять устойчивость (например, в стержневой системе все стержни растянуты), то выдается сообщение, что система "абсолютно устойчива".

                Далее проверяется устойчивость системы при l = L (т.е. положительная определенность матрицы А(L)). Если это условие выполнено, то выдается сообщение о том, что КЗУ больше заданного максимума.

                Если условие положительной определенности А(L) не выполнено (об этом свидетельствуют отрицательные значения на главной диагонали матрицы жесткости, преобразованной в процессе решения системы уравнений), производится анализ положительной определенности матрицы А(L/2),..., т.е. используется стандартный метод половинного деления. Этот процесс продолжается до тех пор, пока не найден интервал (l1, l2) такой, что l2 - l1 £ e и матрица А(l1) положительно определена, а матрица А(l2) этим свойством не обладает. При этом величина l1




считается КЗУ.

                При составлении матрицы устойчивости для каждого конечного элемента (способного терять устойчивость) вычисляется значение lкр, которое приводит к потере устойчивости КЭ. Если min lкр

< L, интервал поиска сокращается, а номер элемента, для которого достигается min lкр, сообщается в протоколе.

13.3 Форма потери устойчивости

В предположении, что определенный на первом этапе коэффициент запаса устойчивости является точным, SCAD производит решение задачи об определении собственного вектора при известном собственном значении задачи



                (A - B(l1)) u = 0.                                   (а)

                Заметим, что правые части системы равны нулю, т.е. отыскиваются такие значения узловых перемещений и пово­ротов u, которые вызываются только внутренними сжимающи­ми напряжениями и усилиями. Поперечные нагрузки, как известно, не влияют на значения критических сил и вид формы потери устойчивости. Поскольку уравнение (а) решено при нулевой правой части, то форма потери устойчивости определена лишь с точностью до множителя. Ее уменьшение или увеличение в любое число раз не нарушает условие (а).

13.4 Свободные длины

Если в системе имеются стержневые элементы, то можно определить их свободные длины, т.е. длины таких же, но шарнирно опертых стержней, у которых критическая сила Nкр совпадает с продольным усилием в стержне системы в момент потери устойчивости (Nкр=l1*N). Поскольку по формуле Эйлера   Nкр = p2EJ / l2, свободная длина будет lo = (l1N

/  p2EJ )1/2,

где EJ ? жесткости стержней в главных плоскостях инер­ции (для пространственной задачи ? по две для каждого стержня).

13.5 Ввод данных

               

Ввод данных для проверки устойчивости выполняется в одноименном диалоговом окне (рис. 13.5.1), которое вызывается из раздела Специальные исходные данные в Дереве проекта. Для ввода данных необходимо выполнить такие операции:

Ä      с помощью комбинаторных кнопок задать режим проверки ? вычисление коэффициента запаса устойчи­вости, форм потери устойчивости и свободных длин стержневых элементов;

Ä      в полях Масштабный множитель и Точность вычислений

следует ввести соответствующие значения (по умолчанию приняты 2 и 0.01);

Ä      активизировать опции, определяющие вид данных, для которых выполняется проверка устойчивости: по загруже­ниям или по комбинациям загружений, для всех загружени­й (комбинаций) или только для выбранных; в послед­нем случае выбор нужных данных выполняется в списке загружений (комбинаций).

Масштабный множитель ? параметр используется для ограничения интервала поиска коэффициента запаса устойчивости. Если его значение больше заданного, система считается устойчивой.

Точность вычислений - параметр задает критерий окончания итерационного процесса поиска коэффициента запаса устойчивости. При очень малых значениях этого параметра время расчета может существенно увеличиться.

                Для удаления подготовленных данных и отказа от анализа устойчивости используется кнопка Удаление данных.





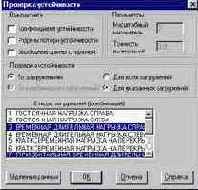
Рис. 13.5.1. Диалоговое окно

Проверка устойчивости


Содержание раздела



---







---